This blog offers an intuitive and engaging introduction to various algorithmic lower-bounding techniques, presented in a playful and interactive manner that anyone—even without a mathematical background—can grasp. The follow-up post will delve into the mathematics behind elegant lower-bounding techniques.

Say suppose you have two methods to solve a problem, both give you the right solution, then when do you call a method better than the other? One measure is, if you get to the solution faster using one method than the other, then the faster one can be called a better method. But what exactly is fast or slow? How to quantify time when it comes to computing?

There are many ways to do this. One way is to count the number of basic operations or steps needed to get to the solution. If your problem instance grows in size intuitively, for most cases, the number of steps needed to get to the solution also increases. To capture this dependence, we give the number of steps to solve a problem in terms of its input size (generally denoted as $n$). This quantity is called the time complexity.

For a given problem, we could have a very dumb way of solving it that takes a zillion steps to get to the solution. At the same time, we might have a very clever way of solving this problem in just 10 steps. Thus, for a given problem, we can have many different methods or algorithms with varied time complexities.

Before talking about how to decide which is the fastest algorithm to solve a given problem, let us build some intution for this. In order to do so I present 2 interactive games in this blog post.

Let’s right away get started with the first game.

Game 1: The Number Guessing Game

I have a number in mind (it is between 1 and 10,000), and you can ask me questions of the following and try to guess the number:

• Is the number greater than $x$? $>x$
• Is the number lesser than $x$? $<x$
• Is the number equal to $x$? $=x$

Your task is to guess the number with the least number of questions. In particular, you win this game if you can find the number with just 14 questions or less (What’s so special with 14? To know this read by follow-up post Knowing When to Stop Looking for Better Ways to Solve Your Problems).

Click here to play the Number Guessing Game

If you took a moment to play the game and returned, how did it go? Were you able to win? If so, what clever strategy did you use to guess the number efficiently?

A very intutive way to get to the number fast is by trying to rule out a large chunk of possibilities after every question. Obviously, asking questions like “Is the number =1?”, “Is it =2?” and so on is not so good. Here, you rule out only 1 number at a time. You would need 100 steps if 100 is the number. So a strategy that gets rid of a large portion of possible numbers with every subsequent question seems to be great.

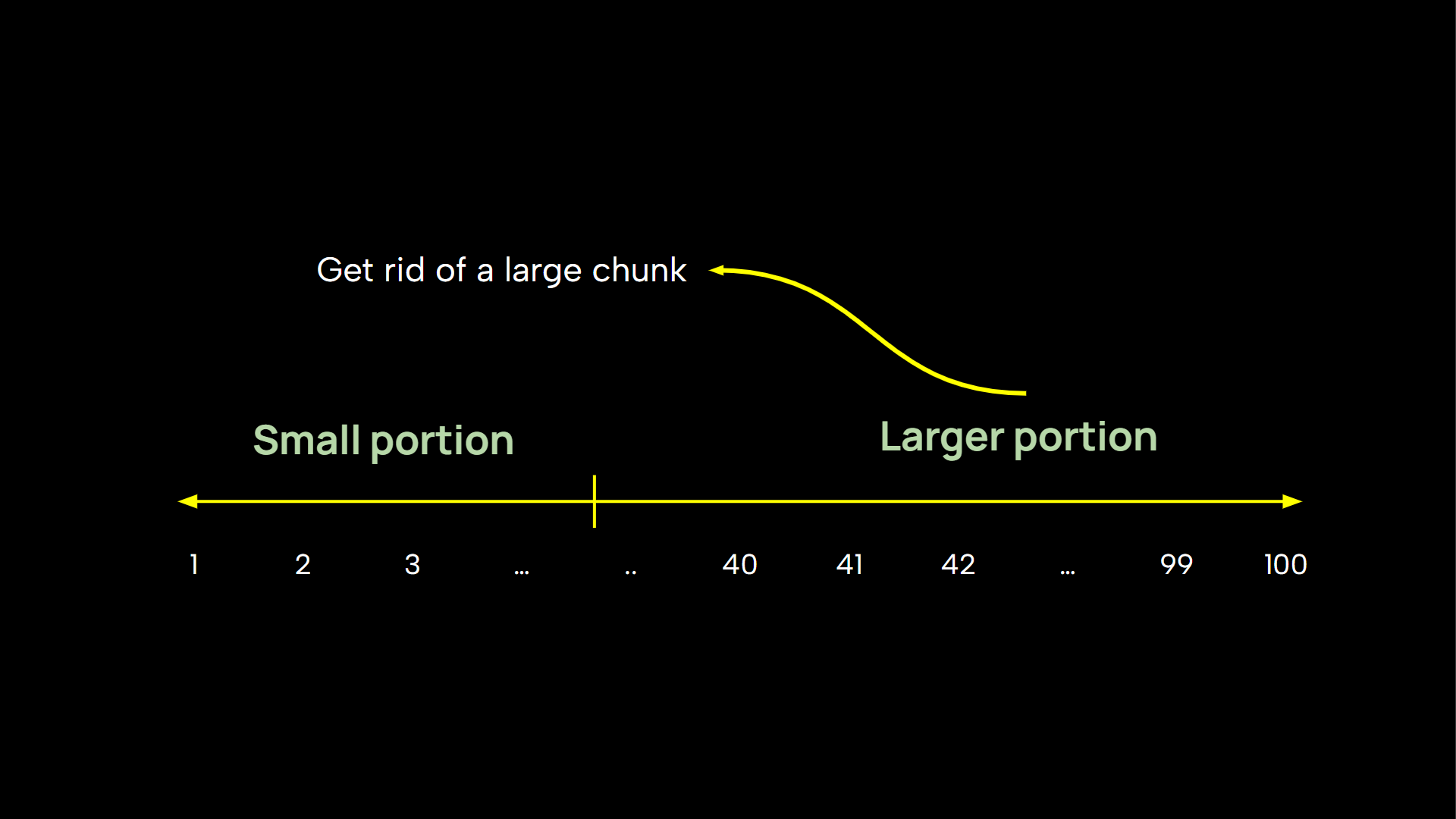
But how much can you throw away at a step? Can you be greedy and try to get rid of almost 90% of the possible candidates?

For that, let’s plan another game.

Game 2: The Guess Blocker Game

This game is like the Number Guessing Game but roles reversed. Here, you can choose any number you want to (between 1 and 10,000). Now I (actually, the computer) will try to guess the number.

Click here to play the Guess Blocker Game

Now assuming that you played the above game, what do you think is a clever blocker’s strategy? What did you do to choose the number?

One cunning strategy to pick a number is, to not pick at all! At every step, when the opponent tries to reduce the possiblities of numbers, you can make sure not to do this. Every time someone asks a question like “Is the number < 70?” and hopes to get rid of all numbers below 70. Here, you can just say no and only reduce the search space by 30. You can go one like this and choose your number at the end, just making sure your answers are consistent.

Initially, after the first game, we discussed the best strategy is to get rid of a large portion at each step. But now we can argue that if one tries to do that, you can always make sure that doesn’t happen. So, what’s the all situation’s best strategy?

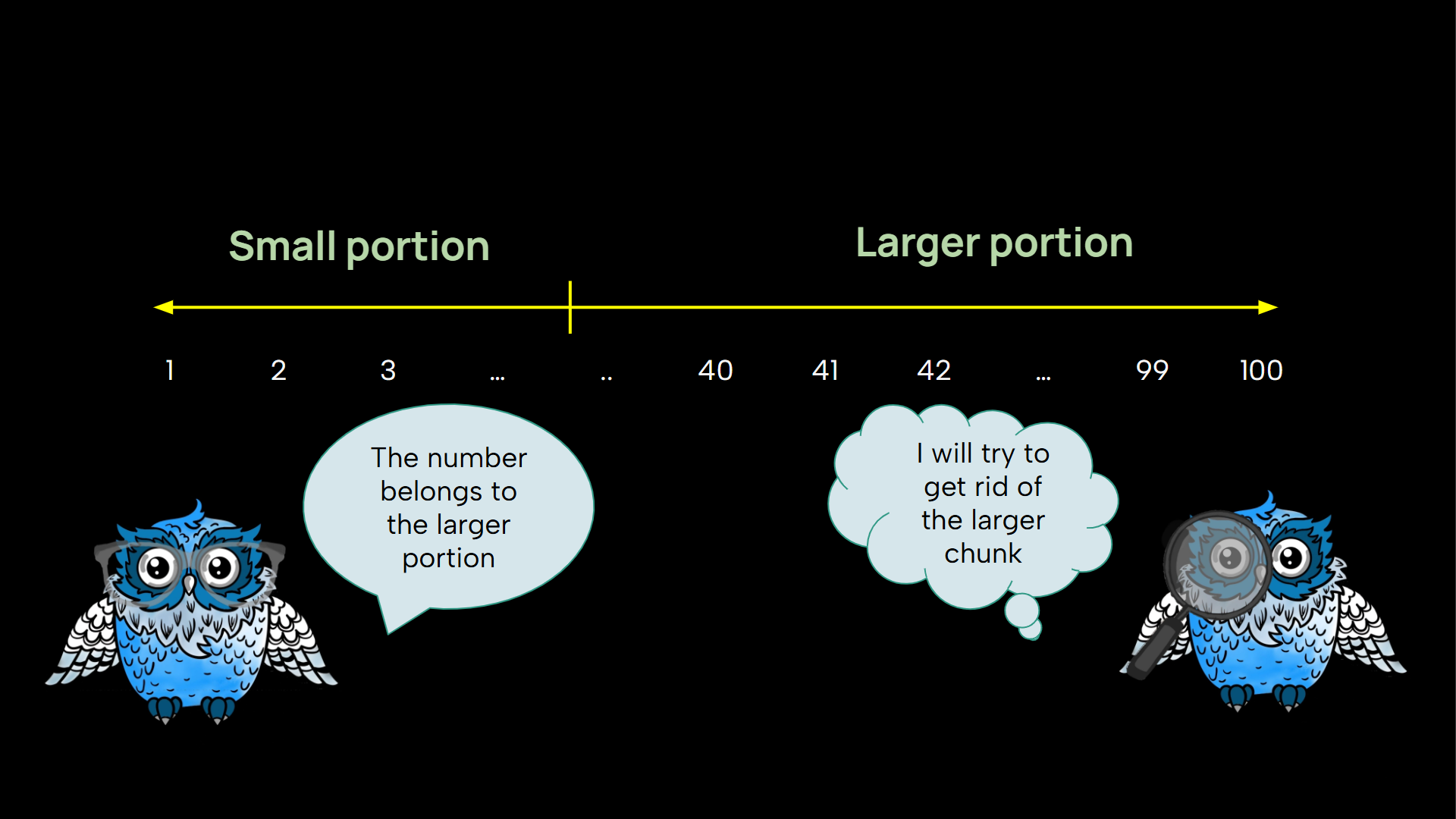
One possible answer to the above question is, what if you also play smart and give the other person no advantage over choosing any portion? By just dividing the possible numbers into two equal halves every time there is no small or large portion to choose from. Let’s call this strategy “divide half”.

But is divide half the best strategy to play the above game?

Now, to your surprise, we can give a rigorous mathematical proof that no matter how clever one is, one cannot come up with a better strategy than our divide half.

The next blog post will present this rigorous yet simple mathematical proof to lower the number of steps needed to win this game.