Quantum Query Complexity
How can we mathematically describe a quantum algorithm? Can quantum advantage help reduce the query complexity to a significant level? What is a quantum oracle? In this blog, I will address these and many other questions about Quantum Query Complexity.
For people familiar with quantum mechanics, you may know that the time evolution operator is unitary. When quantum states evolve, no two input states will evolve to the same output state given a particular Hamiltonian. Thus, in quantum computing, all the gates are unitary transformations. But is classical computing reversible? Are all the classical gates (NOT, AND, OR) reversible in nature? The answer is no.
Note that it is reversible in the sense that, given the output, we can get the input back every single time.
In a classical oracle (black box) model, for input $i$, we get $x_i$ as an output. But this is not a reversible process (we cannot always get $x$ from $f^{-1}(x)$). Since quantum mechanics is reversible, we need a reversible notion of queries to define a quantum oracle.
Consider the following oracle:
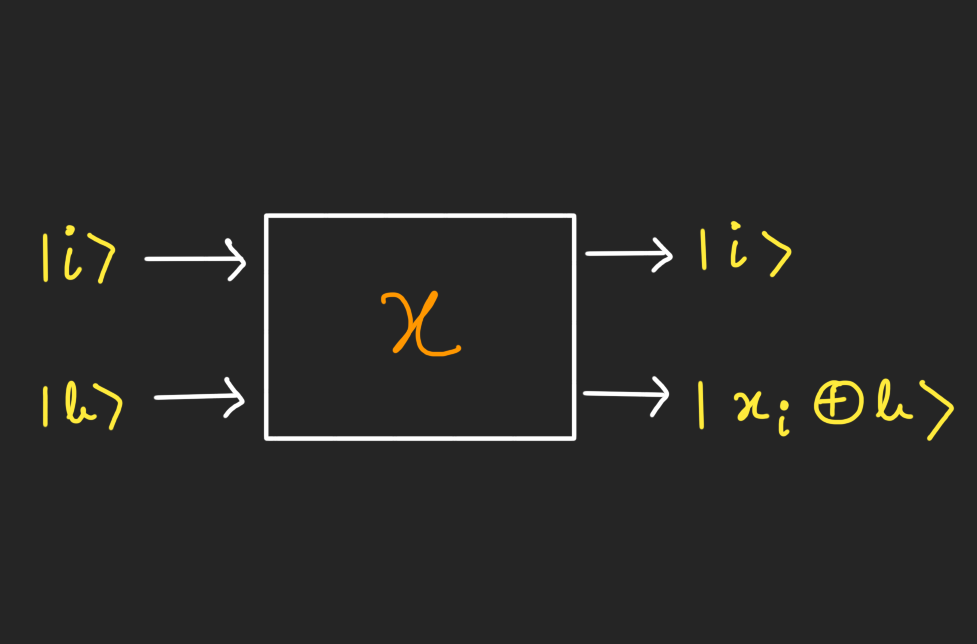
This query maps the pair $(i, b)$ to the pair $(i, b \oplus x_i)$. Here $b \in { 0, 1}$ is an arbitrary bit, which will often be 0, and $b \oplus x_i$ denotes xor of $b$ and $x_i$ (flipping $b$ if $x_i = 1$).
The point of defining a query this way is that it can be reversed. In fact, applying the same oracle again reverses this.
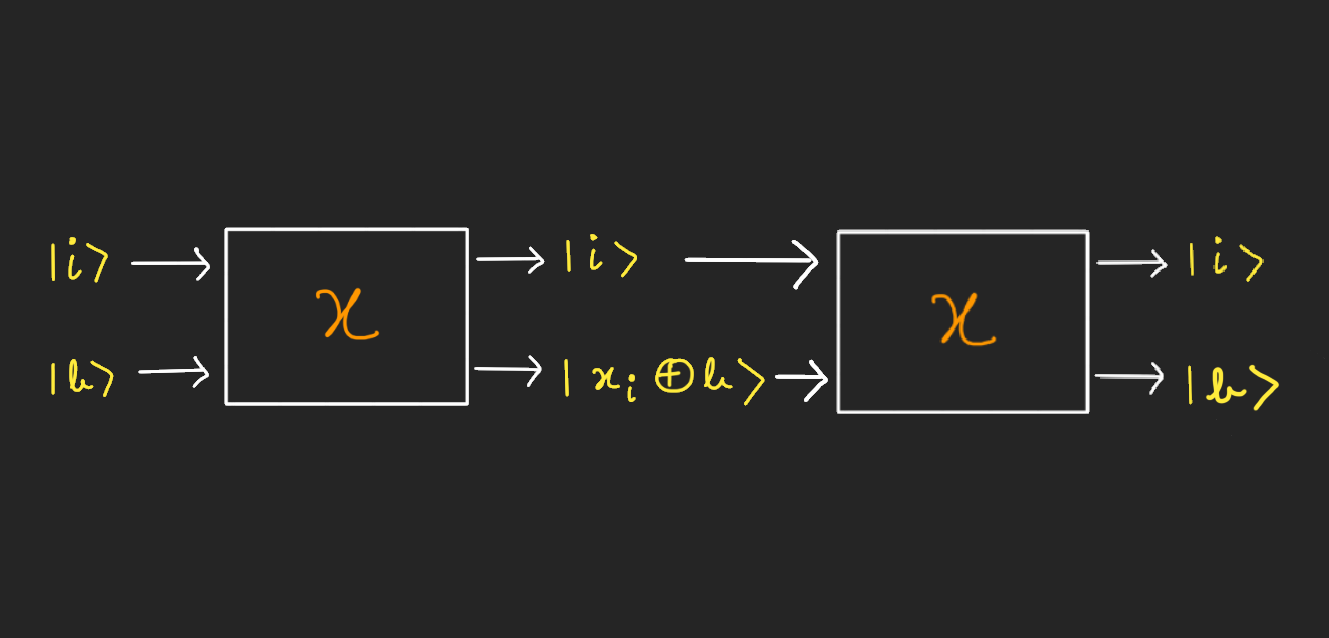
As the second oracle maps $\lvert i \rangle \lvert b \oplus x_i \rangle \rightarrow \lvert i \rangle \lvert x_i \oplus b \oplus x_i\rangle = \lvert i\rangle \lvert b \rangle$
Extras: For more mathematically inclined readers (click to expand)
Note that we can then represent the map $\lvert i\rangle \lvert b\rangle \rightarrow \lvert i\rangle \lvert b \oplus x_i \rangle$ by a matrix $U_x$, which will be a permutation matrix, and therefore is unitary.
A permutation matrix is a square binary matrix with exactly one entry of 1 in each row and each column with all other entries 0. One can easily see that they are unitary matrices (i.e., $UU^\dagger = \mathbb{1}$).
For an oracle that does this
$\lvert i\rangle \lvert b\rangle \rightarrow \lvert i\rangle \lvert b \oplus x_i\rangle$
The matrix element of the oracle $O_x$, $\langle j, c \rvert O_x \lvert i, b \rangle =$
$= \langle j, c \lvert b \oplus x_i \rangle$ (By the action of the oracle, which follows from its definition)
$= \delta_{I,j} \langle j, c \lvert b \oplus x_i \rangle$
$= \delta_{ij} \delta_{c, b \oplus x_i }$
Thus, it is a permutation matrix.
Note that $\delta_{c, b \oplus x_i } = 1$ when $c = b \oplus x_i$
$\implies b \oplus c = b \oplus b \oplus x_i = 0 \oplus x_i = x_i$
Therefore for each block corresponding to a given i, $\delta{ c, b \oplus x_i }$ connects all and only the indices $b,c$ such that $b \oplus c = x_i$
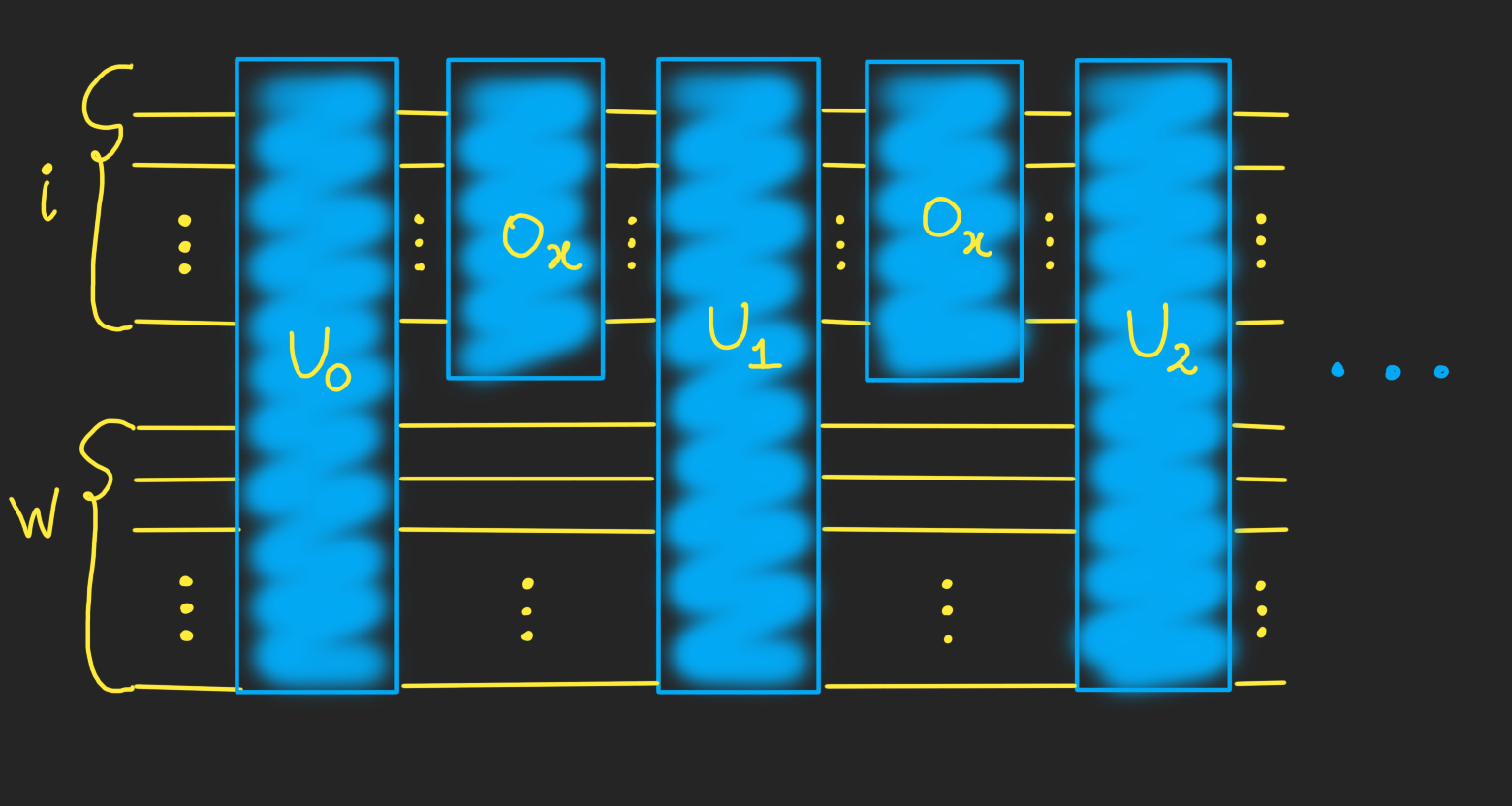
After each query, we would like to allow the quantum algorithm to select the following query arbitrarily. To do so, we give the algorithm a workspace of arbitrary size. That is, let $W$ be a set representing the possible basis states of the workspace. Then, the quantum algorithm will act on the Hilbert space. with basis states corresponding to $W \otimes [n] \otimes { 0, 1}$. In addition to this, we also have an output register. The algorithm will alternate between applying an arbitrary transformation on this state, which is independent of $x$, and applying the unitary $U_x$ implementing the query specified by the query register (the unitary $U_x$ will be extended to act as identity on the workspace register). That is, the action of the quantum algorithm on $x$ will be
$U_T U_x U_{T-1} U_x U_{T-2} U_x \dots U_x U_1 U_x U_0 \lvert \psi_{init}\rangle$ ,
where $\lvert \psi_{init}\rangle$ is some fixed initial state. Note that $T$ is the number of queries the quantum algorithm makes.
We say that a quantum query algorithm $Q$ computes Boolean function $f$ to error $\epsilon$ if $\mathcal{P}[Q(x) \not = f(x)] \leq \epsilon$ for all inputs $x$. It turns out that quantum algorithms can be amplified just like classical ones by repeating the algorithm several times and taking the majority vote on the outputs. For this reason, we will again pick $\epsilon = 1/3$ as the standard choice.
Definition:
Quantum query complexity $\mathrm{Q}(f)$ is defined as the minimum number $T$ such that there is a $T$-query quantum algorithm computing $f$ to error 1/3.
Definition:
$\mathrm{Q}_E(f)$ to be the minimum number $T$ such that there is a $T$-query quantum algorithm computing $f$ to error 0.
In future blog posts, we will look at various quantum query algorithms and see the quantum advantage in action:)
Reference
Shalev Ben-David. Query complexity basis. Lecture notes.
