Deterministic Query Complexity
This is a introduction to Query Complexity Model (also known as Black Box Model). This blog will specifically focus on deterministic algorithms in query model.
In complexity theory, we are interested in quantifying how easy or hard a problem is. Consider your favorite problem. Is the problem easy to solve on your mobile phone or your computer? What if I give you a supercomputer now?
Depending on the device, if your answer changes, given zillion models of electronic devices, we can never objectively classify a problem as easy or hard.
Thus, in complexity theory, we study abstract models of computation. They allow us to compare the hardness of the problem independent of the performing capabilities of a physical computer and enable a clean mathematical description of the problem. In this blog post, I will introduce one such model - Query complexity.
Time complexity is something you might have come across. I plan to post a dedicated blog post on time complexity in the future. When we study time complexity, we assume free access to the input and charge only for the basic operations done on this input. As opposed to this, in a query complexity model, we do not care about the operations done on the input bit but only care about how many times we have to query the input. In this game of query model, we don’t care about any other resources an algorithm uses, like memory or running time, just how many bits of the input it looks at. There are many reasons why, but the simplest is that, unlike with memory or running time, for many functions, we can actually figure out how many input bits need to be looked at without needing to solve anything like P vs. NP. We will see that this itself, though it seems like a simple model, is a non-trivial task.
In the following section, I will define the query model more formally and discuss various algorithms in this model - starting with the deterministic algorithm.
Query Complexity Model
The query complexity model is also called the black box model. One can describe this model in the following way:
Given: a black box $x$
Typically, we will be dealing with Boolean functions, so here $x \in$ {0,1}$^n$
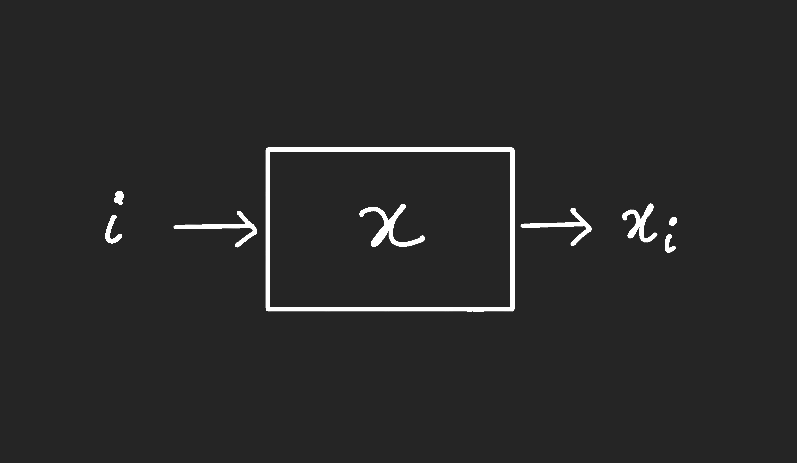
On an input $i$ the black box outputs $x_i$ (this counts as one query), the $i^{th}$ bit of the input string $x$
Goal: To compute $f(x)$, some boolean function $f:${0,1}$^n \xrightarrow{}${0,1}, with a minimum number of queries to the black box.
Let us see how one can describe a deterministic algorithm in a query complexity model.
Deterministic Algorithms
A deterministic algorithm for a given input $x$, irrespective of when and where the algorithm is run, always computes the value of $f(x)$ correctly and in a deterministic way. Given an input $x$, it follows an entirely Deterministic path querying bits of $x$ and, in the end, outputs $f(x)$. This idea can be captured in terms of a decision tree.
Definition: A (Deterministic) decision tree on the input of size n is either a leaf in {0,1} or a tuple $(i, D_0, D_1)$ (represented as a node $x_i$, when its value is 0, it is attached to subtree $D_0$ and when 1, subtree $D_1$) where $i \in [n]$ and $D_0$ and $D_1$ are decision trees which do not use $i$ in any intermediate tuple.
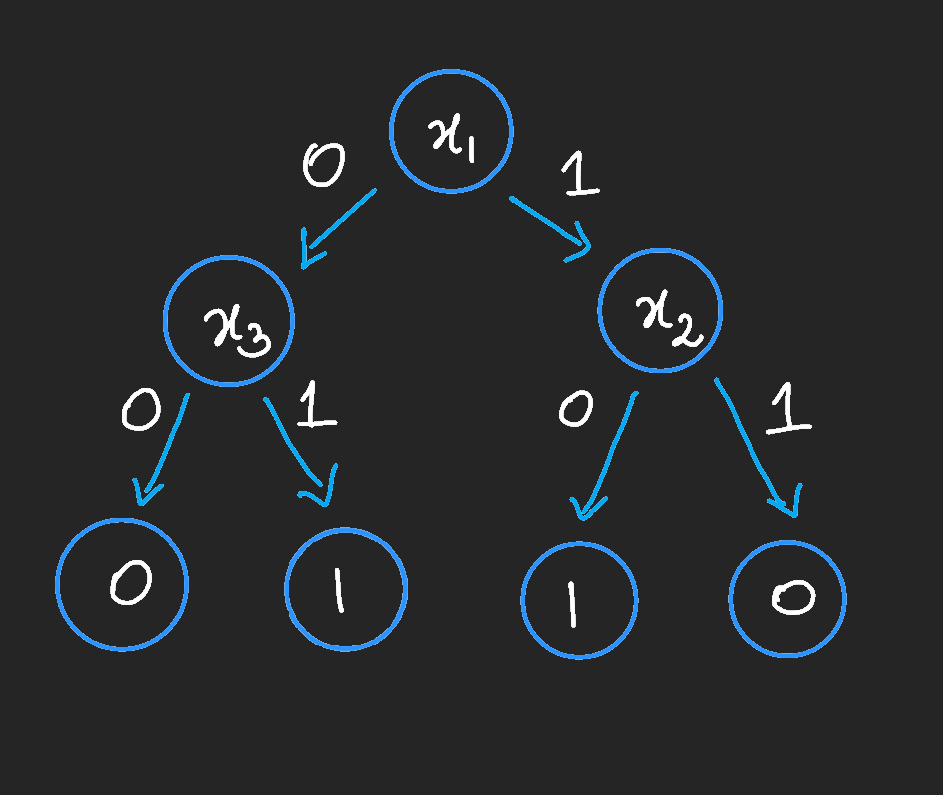
The way this works is as follows: on input $x$, the algorithm starts at the top of the tree, and if the node looks like $(i, D_0, D_1)$, the algorithm queries bit $i$ of $x$ to get the answer $x_i \in ${ 0, 1}. The algorithm then goes to $D_0$ if $x_i = 0$ and to $D_1$ if $x_i = 1$, and repeats the same process there.
A decision tree $T$ is said to compute the value of a function $f$ if and only if $T(x) = f(x) \ \forall \ \ x \ \in$ \ domain($f$).
Height of a decision tree $T$ is the longest root-to-leaf path in $T$.
Note that there can be multiple decision trees computing the function $f$. In this entire query complexity set-up, as our goal is to minimise the number of queries, therefore we pick the decision tree with the least height.
Definition: The Deterministic tree complexity of a function $f$, denoted as $D(f)$, is defined as the height of the best tree computing $f$. \(D(f) = \min_{T} \ ( \max_x \ (path (T,x)) )\) Here, we are taking $\min$ over only those trees $T$ that compute $f$. And $path(T,x)$ is the number of nodes from root to leaf in the path $x$ traces.
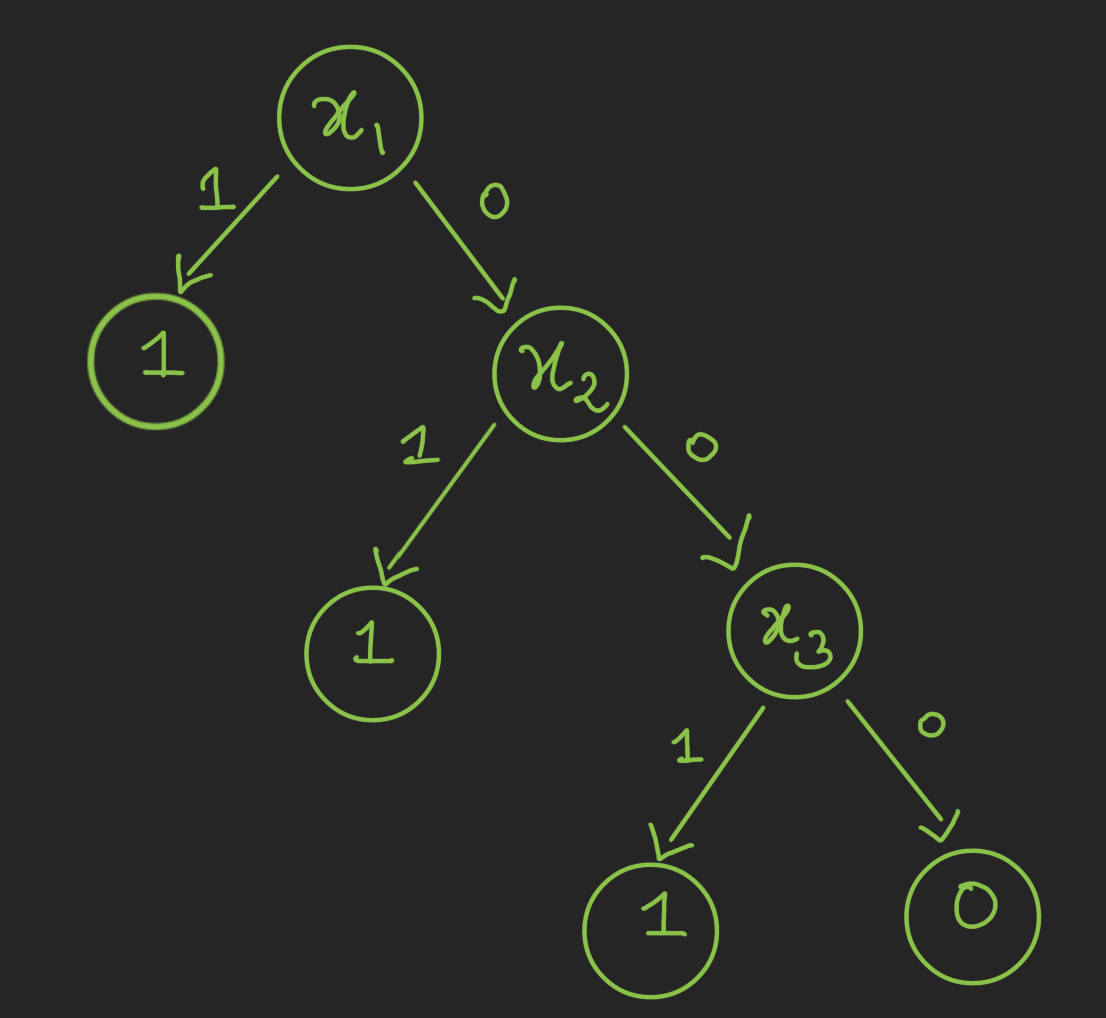
Pause and ponder: Come with a decision tree computing OR function on n = 3 bits Click to expand
If we find 1 at any index then we can halt and output 1 (true).
 (/)
(/)
References
Shalev Ben-David. Query complexity basis. Lecture notes.
Rajat Mittal. Decision tree complexity. Lecture notes
