What is computation? In loose terms, computation is making a physical device (a computer) do some task for us. Things that are hard for humans can be easily done on a computer. So, can computers do anything and everything? Are there things that are hard even for computers? If so, how do we quantify the hardness? Computational complexity theory tries to answer these and even more interesting questions. I would like to give a short bird’s eye view of the field in this blog post.

Computational complexity theory studies the inherent hardness or easiness of computational tasks. Given a task, the field of Algorithms tries to give a clever way of doing that task. There are multiple algorithms for doing the same task. On the other hand, Complexity Theory is interested in providing bounds on a computational task such that no matter how clever one is, one can never come up with an algorithm better than this bound for a given task.

The computational complexity theory field can be broadly classified into two parts.

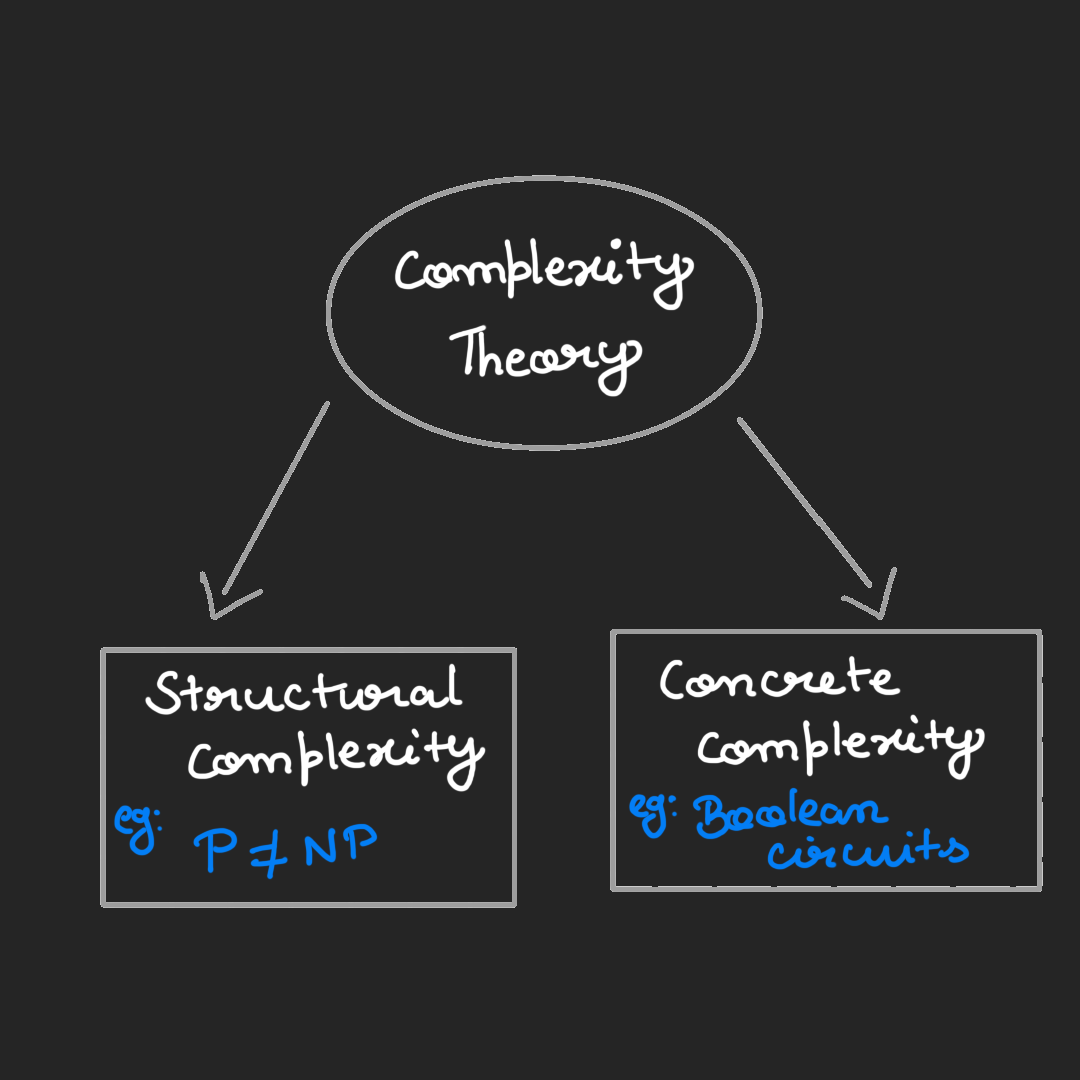
Structural complexity deals with high-level complexity questions. To name a few, it deals with questions like: Is space a more powerful resource than time? Does randomness enhance the power of efficient computation? Is it easier to verify a proof than to construct one? Etc. So far, we do not know the answers to many of these questions; thus, most results in structural complexity are conditional results that rely on various unproven assumptions like $P \neq NP$

Concrete complexity or circuit complexity, as opposed to structural complexity, is a low-level study of computation. It deals with established lower bounds on the computational complexity of specific problems, like the multiplication of matrices, detecting large cliques in a graph or sorting a list. It typically centres around particular models of computation such as decision trees, branching programs, boolean formulas, various classes of boolean circuits, and the like. This line of research aims to establish unconditional lower bounds, which rely on no unproven assumptions.

In the future, you can hope to find individual blog posts on each of the above-stated examples and models of both structural and concrete complexity:)