Dynamic Programming
This is a note on a powerful algorithmic technique called Dynamic Programming
Dynamic programming techniques give a crafty and powerful way of designing algorithms. The basic idea is simple: Given a problem, we break it into subproblems and solve them.
Let us consider a standard example of a dynamic programming algorithm.
Longest increasing subsequence
Given a sequence of positive integers $x_1, x_2, \dots x_n$, find the longest increasing subsequence i.e $x_{i_1} < x_{i_2} \dots < x_{i_m}$ where $i_1 < i_2 \dots < i_m$.
Dynamic programming solution:
Consider the following example:

Here, as the size of the input is small, just by trial and error, we can see that the longest increasing subsequence is
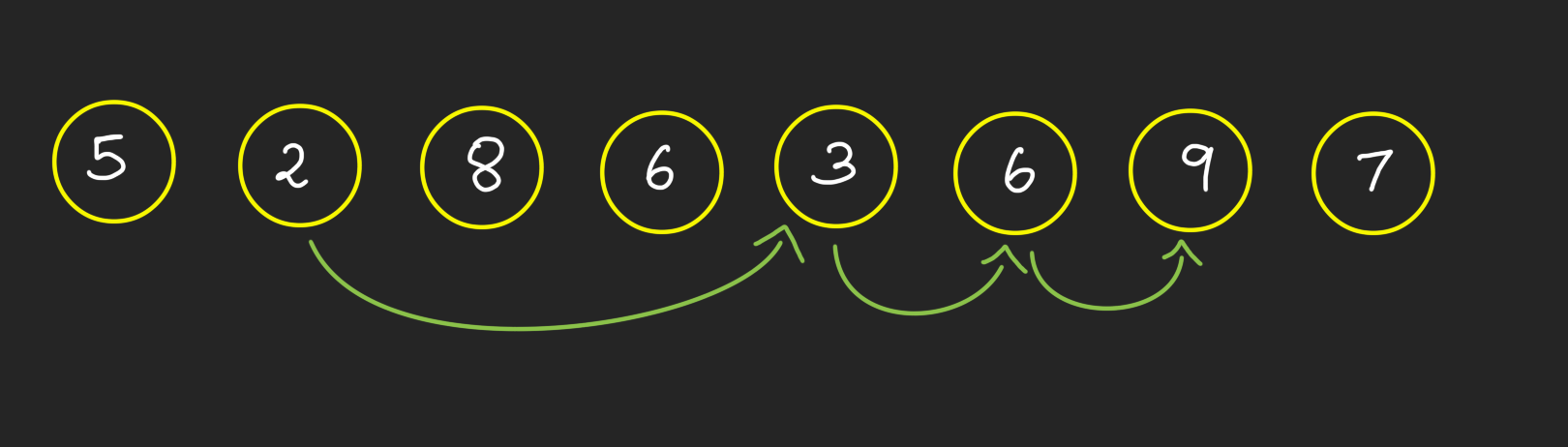
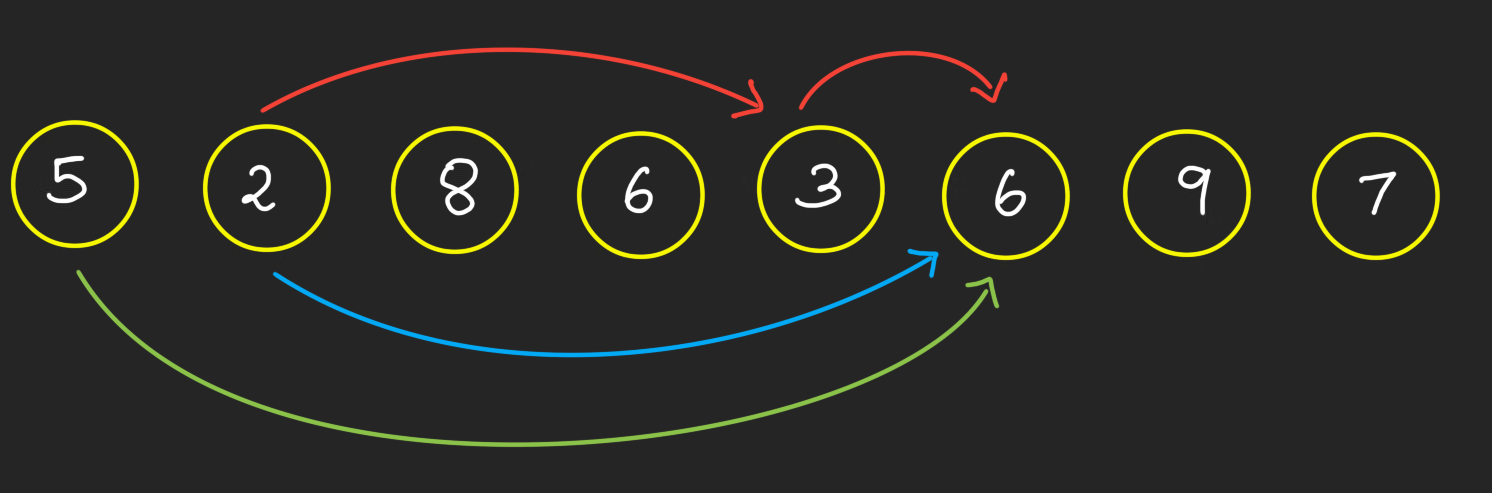
Here are all possible increasing subsequences:
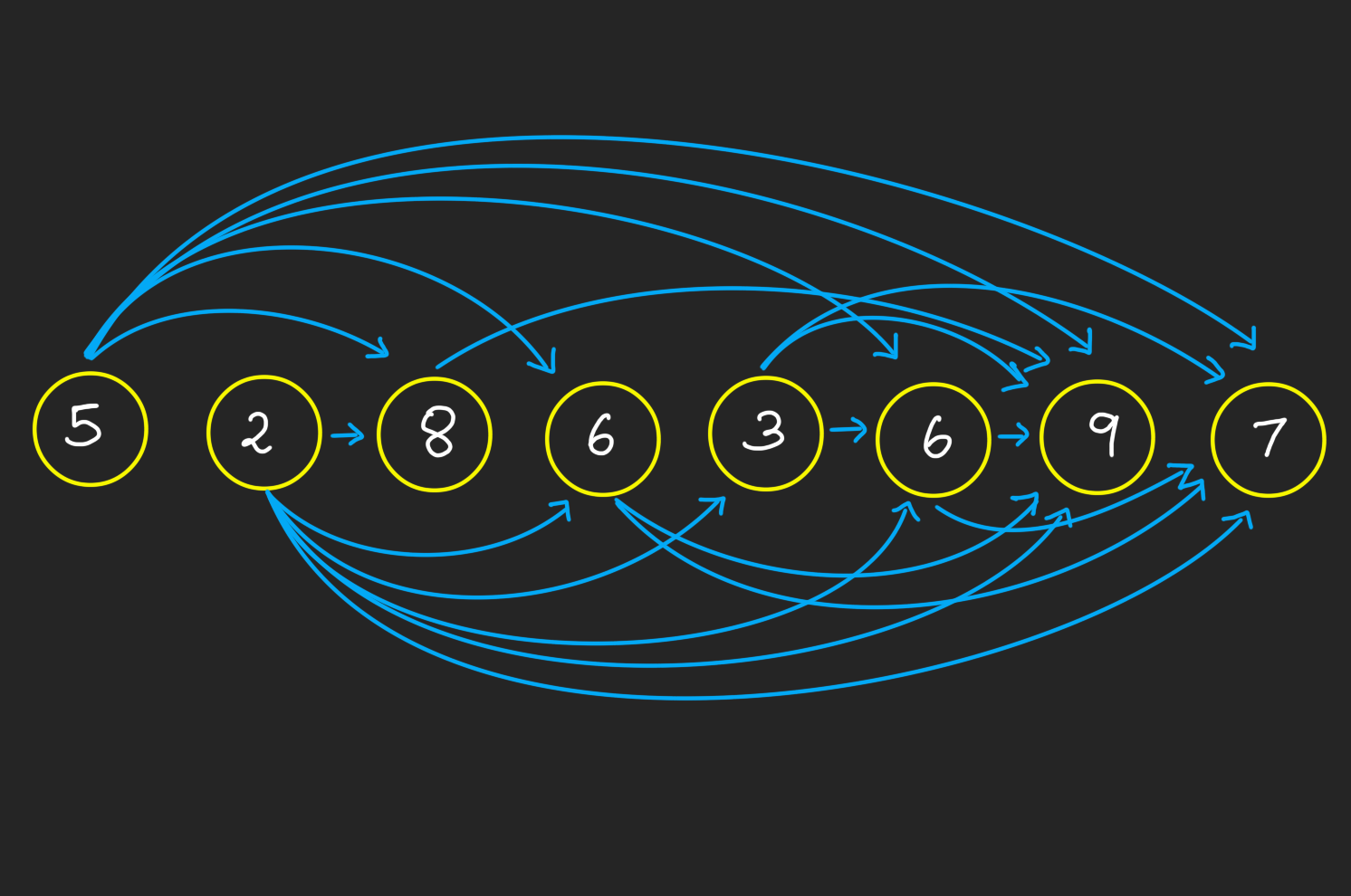
Pause and ponder: Do you notice any stark features of these arrows? Click to expand
They always go from left to right. In graph theory, such a structure is called a Directed Acyclic Graph (DAG). Notice that as the arrows always go from left to right, there are no cycles in such a graph. (No arrows go from right to left to complete a cycle.)
Is there a better way to solve this without trial and error? Most big problems become easy if we make the problem size small.
So, let us start by considering a smaller subproblem. Note that the subproblem does not need to be the same as our orginal problem. It can be a modified new problem on a smaller size of input that ultimately leads to solving our main problem.
In our example problem, let us terminate our sequence at some point and find the longest subsequence ending at that point.
For the first of such case (base case), i.e. when 𝑛=1 The longest increasing subsequence ending at index 1 is the number itself. So the length is 1.
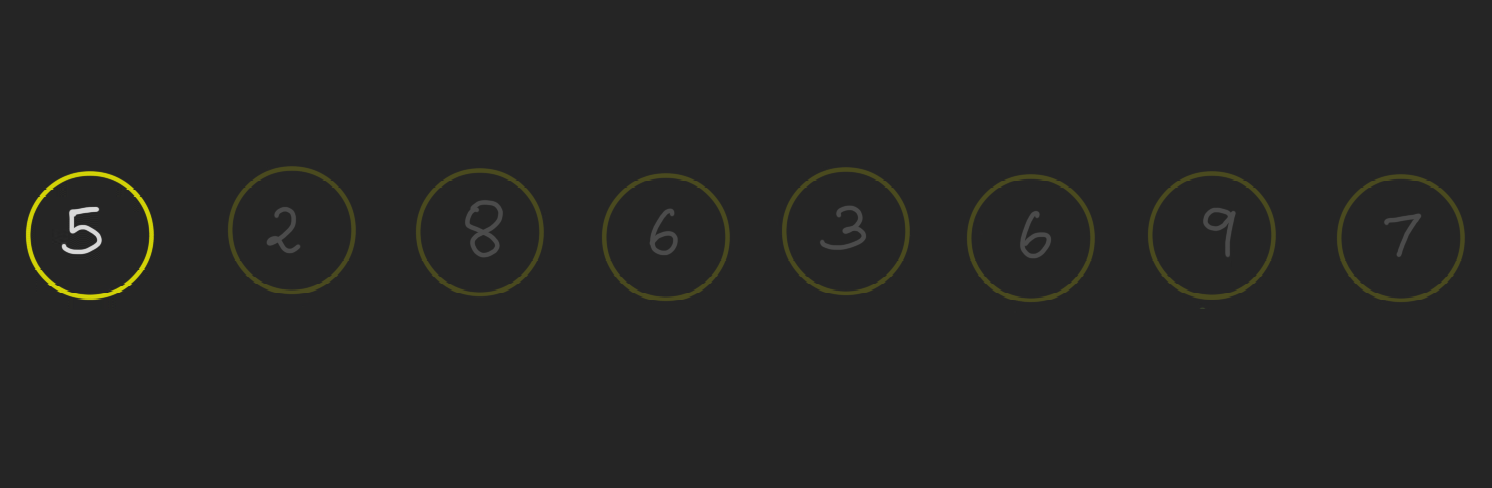
Now, we can increase the value of $n$ one by one and see the length of the longest increasing sequence. For instance, when $n=i$, say 6 (at this point, we assume we have computed the length of the longest increasing subsequence ending at $x_i$ for all $i\leq 5$).
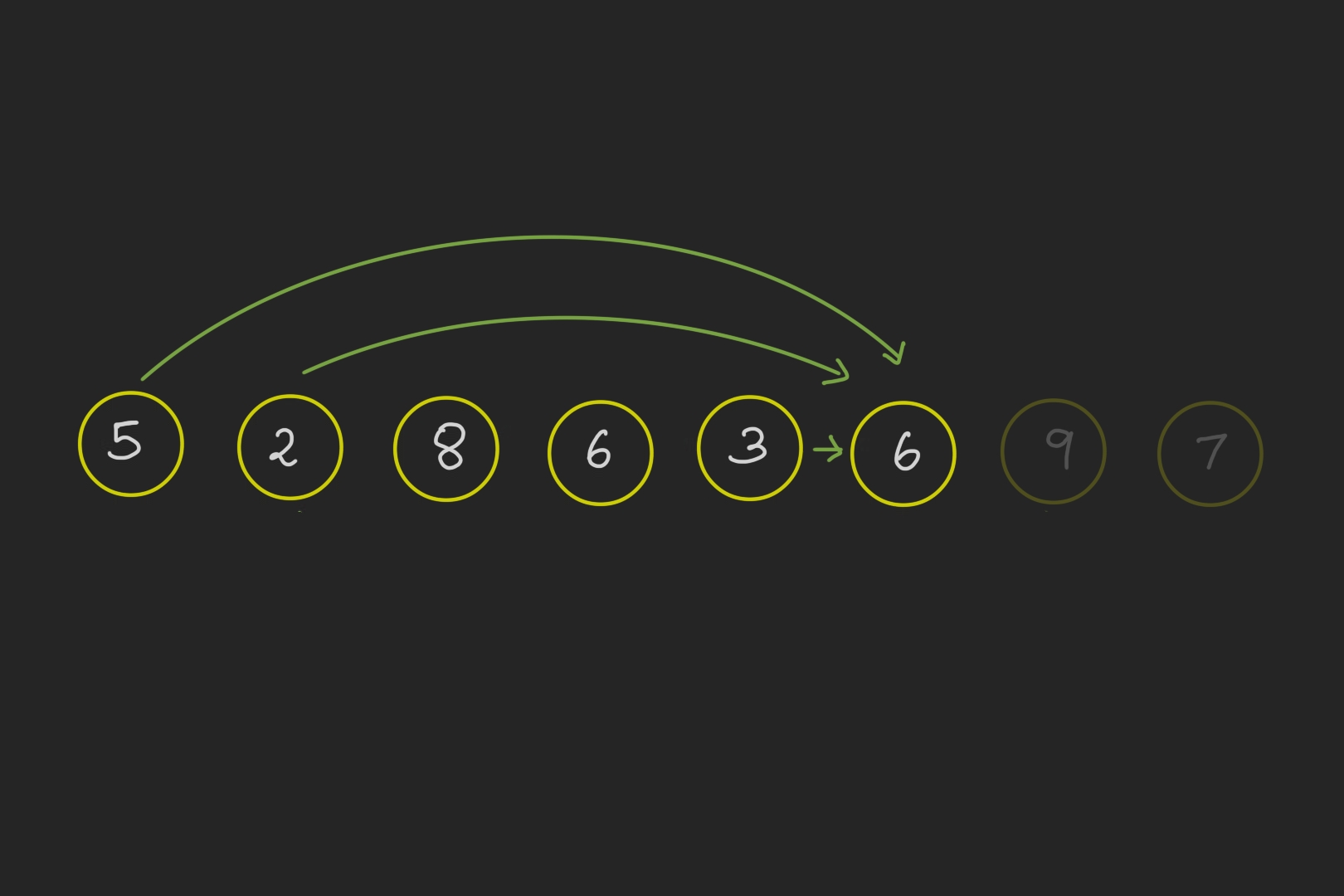
How would one naturally go about finding the longest increasing subsequence ending at index 6? We have the number 6 at position 6. If our sequence should necessarily end at 6, then (as it is an increasing sequence) all numbers to the left of 6 in the sequence shoule be $x_i < 6$. So, either 3, 2 or 5 can come before 6. We want to get the longest sequence possible.
So, it makes sense to pick 3 as it has the longest subsequence ending where it is. (The subsequence being 2-3-).
Like this we can keep going and find the longest increasing subsequence ending at the last number, here $x_8 = 7$.
So, what should we output now?
Pause and ponder: Do we need to output the last computed value, i.e., the longest increasing subsequence ending at 𝑥8? (Click on the answer)
Yes!
Oops:( Go back and refer to the problem statement once.
No
You are right! The question is to find the longest increasing subsequence of the given sequence and not the one ending at the last index.
We need to output the maximum value of the longest increasing subsequence ending at $x_i$ where $i$ ranges from 1 to 8.
Pseudo code
Thus, the above idea can be formalised as follows:
Algorithm pseudo code:
Let L(j) = length of the longest increasing subsequence ending at j
for j = 1, 2, ... n:
L(j) = 1 + max_i{ L(i) : (i,j) ϵ E}
return max_j(L(j))$(i,j) \in E$ refers to all i with an arrow to j, i.e. all numbers to the right of $x_j$ less than $x_j$.
Analysing the time complexity
In the above pseudo-code, $j$ goes over all n, and the $max_i$ goes over all $i$ that has an arrow to $j$ (at max the degree of $j$, in graph theory terms), so it can be at max $n$.
Thus the overall time complexity is $O(n^2)$
Pause and ponder: Can you think of a finer analysis that gives linear time in number of vertices and edges? Click to expand
Note that the at every vertex $j$ max goes over the left neighbours of $j$, which is at max degree of $j$. Thus sum over the degrees of vertices gives 2 X number of edges (by handshaking lemma). Thus the over all time complexity is $O(n+m)$.
Also note here the graph is directed, so it is not straight forward to talk about left neighbours of $j$. One can show that in linear time we can construct the adjacency list of the reverse graph. As an exercise think how this can be done?
DAG structure
In the above pause and ponder, I highlighted that the arrows always go from left to right, forming a DAG structure. This is not unique to this problem alone. In fact, for every dynamic programming problem, there will be an underlying DAG structure - either directly seen or hidden in disguise. This is because the core idea of dynamic programming is first solving a sub-problem and using its solution to solve the next sub-problem, thereby finally building to solving our original problem. The ith subproblem can depend only on previously solved i-1 subproblems and not on something which is not yet solved. Thus, the DAG structure arises as a natural consequence of the core idea of dynamic programming.